Forecasting: Principles and Practice 2nd Edition을 공부한 내용을 기록, 정리하고 있습니다.
5.6 회귀로 예측하기
회귀 모델을 이용해 y의 예측값을 얻을 수 있다.

일단 제일 끝에 붙던 오차항은 예측할 수 있는 범위의 바깥에 있으므로 제외한다. 위 예측변수(predictor variables) 값들을 회귀모델 식에 넣으면 y의 적합값(fitted value)를 얻을 수 있다.
사전 예측 과 사후 예측
사전예상값(ex-ante forecast)
현재 이용할 수 있는 데이터, 즉 과거~현재까지의 데이터만 사용해서 내는 예측값(사전예상값)을 만든다. 이를 계산하기 위해서는 회귀분석 모델의 예측변수 predictor variable 들의 예상값이 필요하다. 이런 예측변수들의 예상값은 과거~현재까지의 값의 평균이나, 랜덤워크로 값을 내거나, 정부기관에서 발표하는 예상값 같은 정보가 있다면 그걸 쓰기도 하는 등 다양한 방법이 있다.
사후예상값(ex-post forecast)
예측변수 predictor variable의 현재값의 이후 정보로 내는 것이다. 예를 들면, 이미 예측변수들의 관측값이 찍히고 난 뒤에 그 관측값을 사용해 예측을 하는 방식으로, 100% 순수한 예측이라고 하기는 좀 그럴수 있지만, 예측 모델의 행동을 관찰하는데는 도움이 된다.
사후예상값을 사용한 모델은 예측하고자 하는 기간의 y 데이터를 가지고 예측하면 안된다. 사후예상 모델은 예측변수 x들의 값을 알고 있다고 가정하지만, 예측해야하는 y값들의 정보는 모르는 것으로 친다.
x, y 둘다 예측값을 쓰는 사전예상 모델과 이미 기록된 x값을 사용해 y를 예측하는 사후예상 모델을 비교하는 것은 예측의 불확실성이 어디서 오는지 파악하는데 도움이 된다. 모델 자체가 예측력이 떨어지는 것인지, 아니면 사용하고 있는 예측변수들의 예상값들이 잘못된 것인지 파악할 수 있다.
소비 증가율 예측 데이터 예시
소득과 저축이 0.5%~1% 정도 증가하거나, 혹은 반대로 감소할 경우를 나눠서 상정한다. 실업률은 그대로라고 가정한다. 예측에 사용하는 예측변수는 소득, 저축, 실업률이다. 아래 코드가 채용하고 있는 방식은 사후예상값을 사용한 모델이다.
## 모델 만들기
fit.consBest <- tslm(
Consumption ~ Income + Savings + Unemployment,
data = uschange)
h <- 4
## 소득, 저축, 실업률이 상승했다고 가정
newdata <- data.frame(
Income = c(1, 1, 1, 1),
Savings = c(0.5, 0.5, 0.5, 0.5),
Unemployment = c(0, 0, 0, 0))
fcast.up <- forecast(fit.consBest, newdata = newdata)
## 소득, 저축, 실업률이 하락했다고 가정
newdata <- data.frame(
Income = rep(-1, h),
Savings = rep(-0.5, h),
Unemployment = rep(0, h))
fcast.down <- forecast(fit.consBest, newdata = newdata)
## 아래 autolayer에서 PI 옵션으로 예측구간도 넣고 있다.
autoplot(uschange[, 1]) +
ylab("% change in US consumption") +
autolayer(fcast.up, PI = TRUE, series = "increase") +
autolayer(fcast.down, PI = TRUE, series = "decrease") +
guides(colour = guide_legend(title = "Scenario"))
예측 회귀모델 만들기
회귀모델의 강점: 예측을 함과 동시에, 예측하고자 하는 변수 y와 예측변수 x간의 주요한 관계를 파악할 수 있다는 점이다. 하지만 사전예상값을 사용해 예측을 하기 위해서, 각각의 예측변수에 대한 예측값도 필요하다는 점이 해결해야 할 문제거리가 된다. 위 예시처럼, 상승 시나리오와 하락 시나리오를 가정하는 등의 시나리오 예측법에 대해선 꽤 유용하게 사용할 수 있다.
대안이 될 수 있는 방법: 과거의 시차값 (lagged values)을 예측변수 x로 사용하는 것이다. 가령, h 스텝의 예측치를 쓴다면 아래의 공식을 사용해 현재값을 포함해 h일치의 과거 기록을 예측변수로 사용하는 것이다.

예측구간 (prediction intervals)
회귀 오차(regression errors)가 정규 분포를 따른다고 가정하면, 95%의 예측구간은 아래처럼 계산합니다.

T는 전체 관측값 수, s(x)는 관측된 x값의 표준 편차, sigma(e)는 회귀의 표준 오차 (standard error of regression). 만약 실제값 x가 x의 평균값과 차이가 많이 나면, 위 산식에서 분자의 크기가 커지게 되어 예측구간이 넓어지게 된다. 예측 변수 predictor variable의 값이 표본의 평균에 가까워질수록, 예측구간이 좁아져 예측값에 대한 확신도 커진다. 위에서 봤던 소비 예제 코드에 예측구간을 구하는 것도 포함되어 있다.
5.8 비선형 회귀
종종 예측분석을 할때 비선형 형태가 더 적당하기도 하다. 비선형관계를 모델링하는 가장 단순한 방법은 y 또는 x를 변환하는 것이다(둘다 변환하기도 한다). 가장 많이 사용하는 것은 자연로그. 만약 x, y 둘다 로그를 씌우게 될 경우 단순선형회귀 공식은 아래처럼 변한다.

x, y에 로그를 씌우면 원래 데이터와 단위가 바뀌기 때문에 계수를 해석하는 데도 방법이 달라진다. 위 모델에서 기존의 계수 beta1은 x가 1단위만큼 증가할때의 y의 변화 정도였다면, 여기서는 x가 1% 증가할 때의 y의 변화 %이다.
로그 변환의 조건
모든 관측값이 0보다 커야 한다.
변수x = 0이라면 log(x+1)로 바꿔준다.
물론, 로그 변환 말고 다양한 변환이 필요할 수도 있다. 일단 모종의 변환을 적용한 함수 f(x)를 임의로 사용하자. 여기서 f(x)

여기서 f(x)는 비선형 공식이다. 이거를 선형회귀 공식으로 나타내면 아래와 같이 표현할 수 있다. 이 f함수는 로그나 다른 변환에 비해 더 유연하게 적용할 수 있는 함수라고 가정할 수 있다.

조각별 선형 piecewise regression
f함수의 가장 간단한 항목 중 하나는 이거를 조각조각 내서 사용하는 조각별 선형 piecewise linear가 있다. 조각별 선형의 경우, f함수의 기울기 beta1이 계속해서 변할 수 있다. 이 변하는 변곡점들을 매듭(knot)이라고 부른다. 먼저 x를 쓰고, x-c = x(2)를 정의하는데, 가령 아래처럼 x(2)의 값은 양일때 x-c의 값을 가지며, 그 외는 0의 값을 가진다는 의미이다.

따라서, c값을 기점으로 기울기가 바뀌게 된다. 이런식으로 x(3), x(4), ... 등을 추가함으로써 변곡점을 여러개 사용할 수도 있다.
회귀 스플라인 regression spline
위에서 살펴본 조각별 선형은 회귀 스플라인의 일종이다. 일반적으로, 선형회귀의 스플라인은 아래처럼 구한다. 아래에서 c(1), ... , c(k-1)은 매듭(선이 구부러지는 점)이다. 이런 매듭의 갯수를 정하거나, 매듭의 위치를 정하는 일은 꽤 어렵고, 임의로 정해서 쓰기도 한다.

조각별 선형보다, 제곱을 거듭하는 스플라인(cubic spline)이 보다 매끄러운 결과를 주기도 한다. 일반적으로, cubic spline은 아래처럼 사용할 수 있으며, 일반적으로 회귀 스플라인보다 더 좋은 예측값을 가져온다. 하지만, 과거의 x값의 범위를 벗어난 y의 예측은 잘 못한다는 단점이 있다.

비선형 트렌드 예측하기
이제 위에서 다룬, 시간별로 구부러지는 조각별 선형을 사용해서 비선형 트렌드를 예측해보자. 만약 이 트렌드가 어떤 특정 포인트 타우에서 구부러진다 가정하고, 해당 시간의 x=t와 c=tau 를 위 조각별 선형식에 대입해, 아래의 공식을 도출했다.
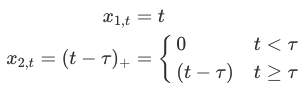
x1, x2의 계수는 각각 beta1, beta2이며, 매듭이 발생하는 타우 점의 이전의 기울기는 beta1이, 타우 점 이후의 기울기는 beta1 + beta2로 계산된다.
보스턴 마라톤 우승시간 예제
1924년에 마라톤 거리가 늘어났기 때문에 우승에 걸리는 시간이 증가했지만 이후에는 내림세이다. 따라서 이 시점을 기준으로 데이터를 구분해보자. 아래 두 그래프중 위에 있는 그래프는 선형회귀 모델값을 표시한 것이고, 두번째는 위쪽 그래프에 있는 모델의 잔차값을 그린 것이다. 첫번째 그래프에서 보다시피, 원 데이터는 직선형이라기보단 곡선이 보이는 비선형 모양이다. 아래쪽 그래프에서 우리는 1980년대 이후 잔차의 분산이 감소하는 걸 확인할수 있다. 잔차가 일정하지 않다.
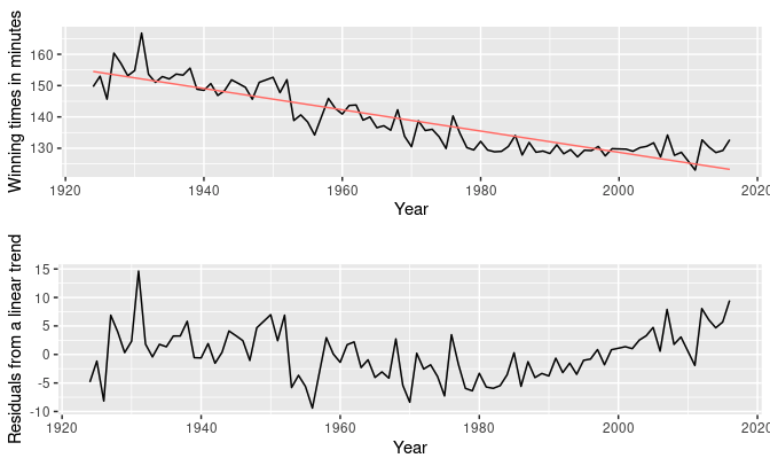
위 그래프에서 가만 보면 1950년 이전까지는 데이터의 변동이 크며, 이후에 거의 선형적인 모습으로 줄어들다가, 1980년대 이후에는 좀 평평한 모습을 볼 수 있다. 따라서 1950, 1980 두 지점을 매듭으로 정해보자. (주의: 이런 주관적인 방식으로 매듭을 정하는 것은 과적합의 오류를 생성할 수 있다)
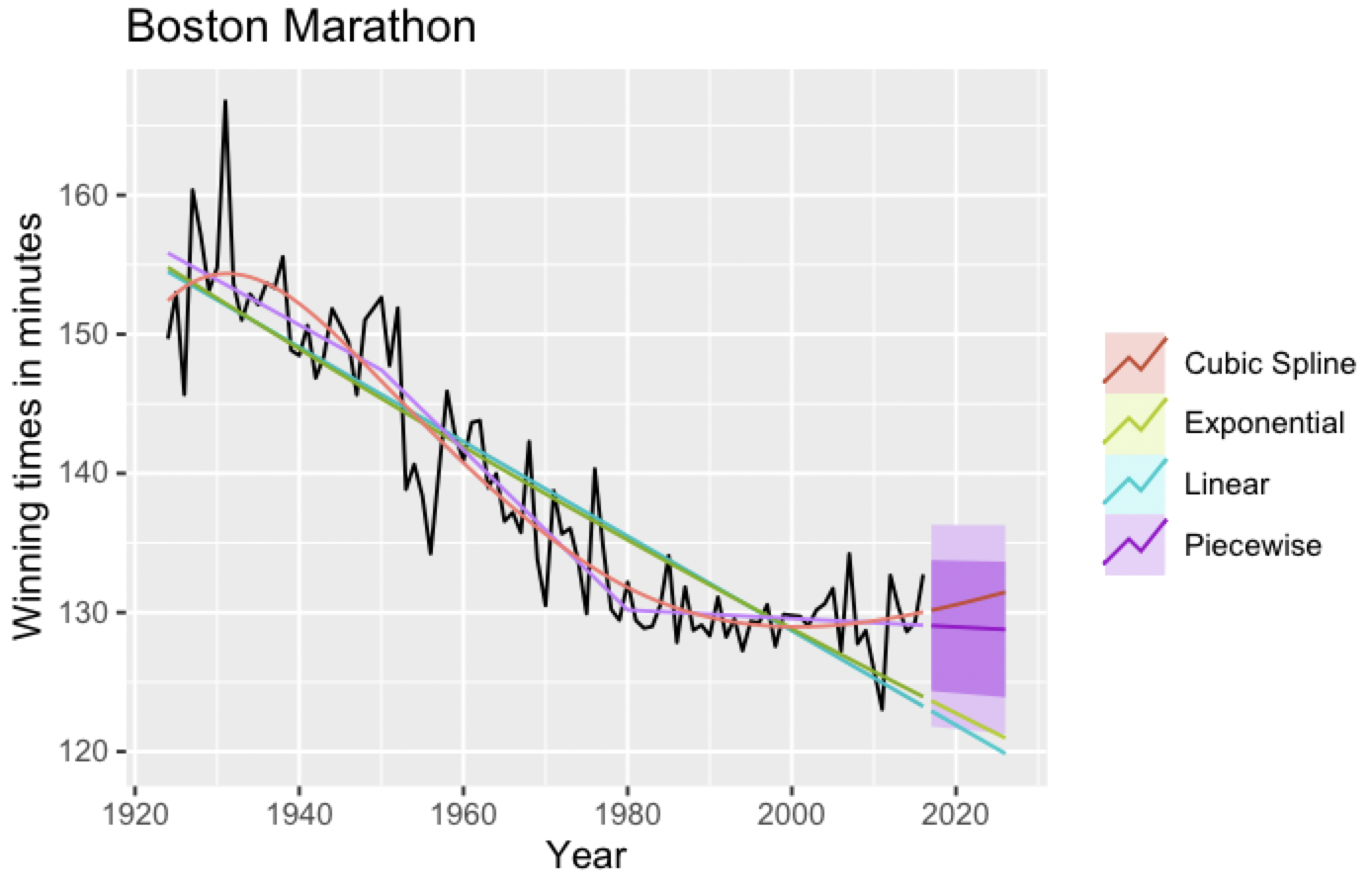
아래는 각각 cubic spline, exponential, linear, piecewise 로 구현한 예측이다. 조각별선형 piecewise가 예측은 제일 잘 하지만, 과거값을 잘 맞추는것은 cubic spline이다.
boston_men <- window(marathon, start=1924)
h <- 10
fit.lin <- tslm(boston_men ~ trend)
fcasts.lin <- forecast(fit.lin, h = h)
fit.exp <- tslm(boston_men ~ trend, lambda = 0)
fcasts.exp <- forecast(fit.exp, h = h)
## tb1: ~1950, tb2:~1980
t <- time(boston_men)
t.break1 <- 1950
t.break2 <- 1980
tb1 <- ts(pmax(0, t - t.break1), start = 1924)
tb2 <- ts(pmax(0, t - t.break2), start = 1924)
## 매듭으로 구간이 나눠진 데이터를 만들기
fit.pw <- tslm(boston_men ~ t + tb1 + tb2)
t.new <- t[length(t)] + seq(h)
tb1.new <- tb1[length(tb1)] + seq(h)
tb2.new <- tb2[length(tb2)] + seq(h)
newdata <- cbind(t=t.new, tb1=tb1.new, tb2=tb2.new) %>%
as.data.frame()
## 제곱으로 예측하기
fcasts.pw <- forecast(fit.pw, newdata = newdata)
## 회귀 스플라인 사용
fit.spline <- tslm(boston_men ~ t + I(t^2) + I(t^3) +
I(tb1^3) + I(tb2^3))
fcasts.spl <- forecast(fit.spline, newdata = newdata)
## 시각화 플롯
autoplot(boston_men) +
autolayer(fitted(fit.lin), series = "Linear") +
autolayer(fitted(fit.exp), series = "Exponential") +
autolayer(fitted(fit.pw), series = "Piecewise") +
autolayer(fitted(fit.spline), series = "Cubic Spline") +
autolayer(fcasts.pw, series="Piecewise") +
autolayer(fcasts.lin, series="Linear", PI=FALSE) +
autolayer(fcasts.exp, series="Exponential", PI=FALSE) +
autolayer(fcasts.spl, series="Cubic Spline", PI=FALSE) +
xlab("Year") + ylab("Winning times in minutes") +
ggtitle("Boston Marathon") +
guides(colour = guide_legend(title = " "))
반면, cubic spline의 대안이 될 수 있는 natural cubic smoothing spline이 있는데, 일종의 제약을 걸어서 마지막에는 spline 공식이 곡선이 아닌 직선으로 끝나게 만들어, cubic spline의 예측력을 높이는 방식이다. splinef() 함수로 쉽게 구현할 수 있다. cubic spline과 비슷하게 과거의 변곡점을 잘 맞추므로, 매듭의 위치를 주관적으로 정하지 않아도 된다는 장점이 있다.
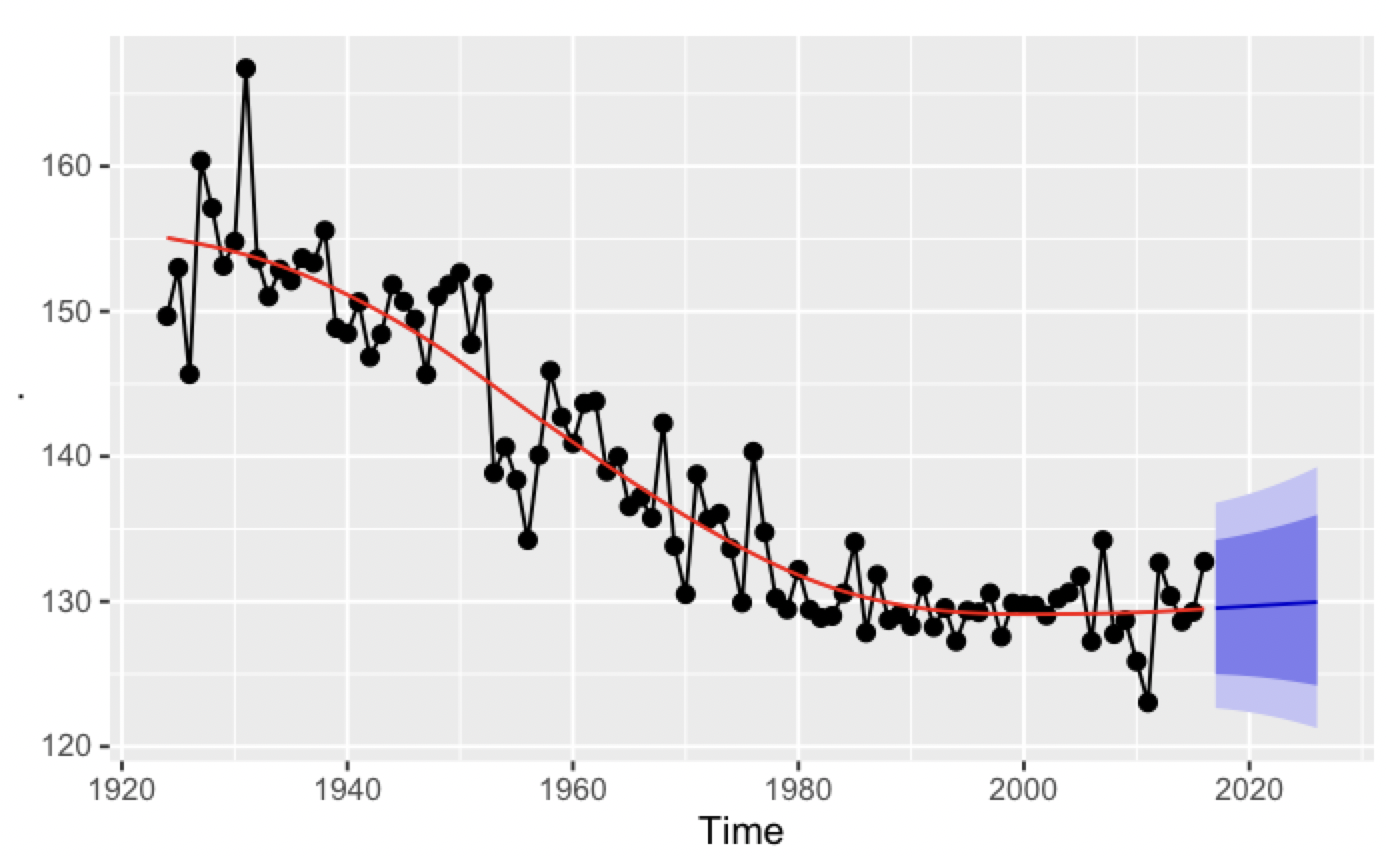
boston_men %>%
splinef(lambda=0) %>%
autoplot()
아래 시각화는 natural cubic smoothing spline의 잔차를 평가한 것인데, 잔차를 일정하게 만들기 위해 lambda = 0으로 로그변환을 했다.
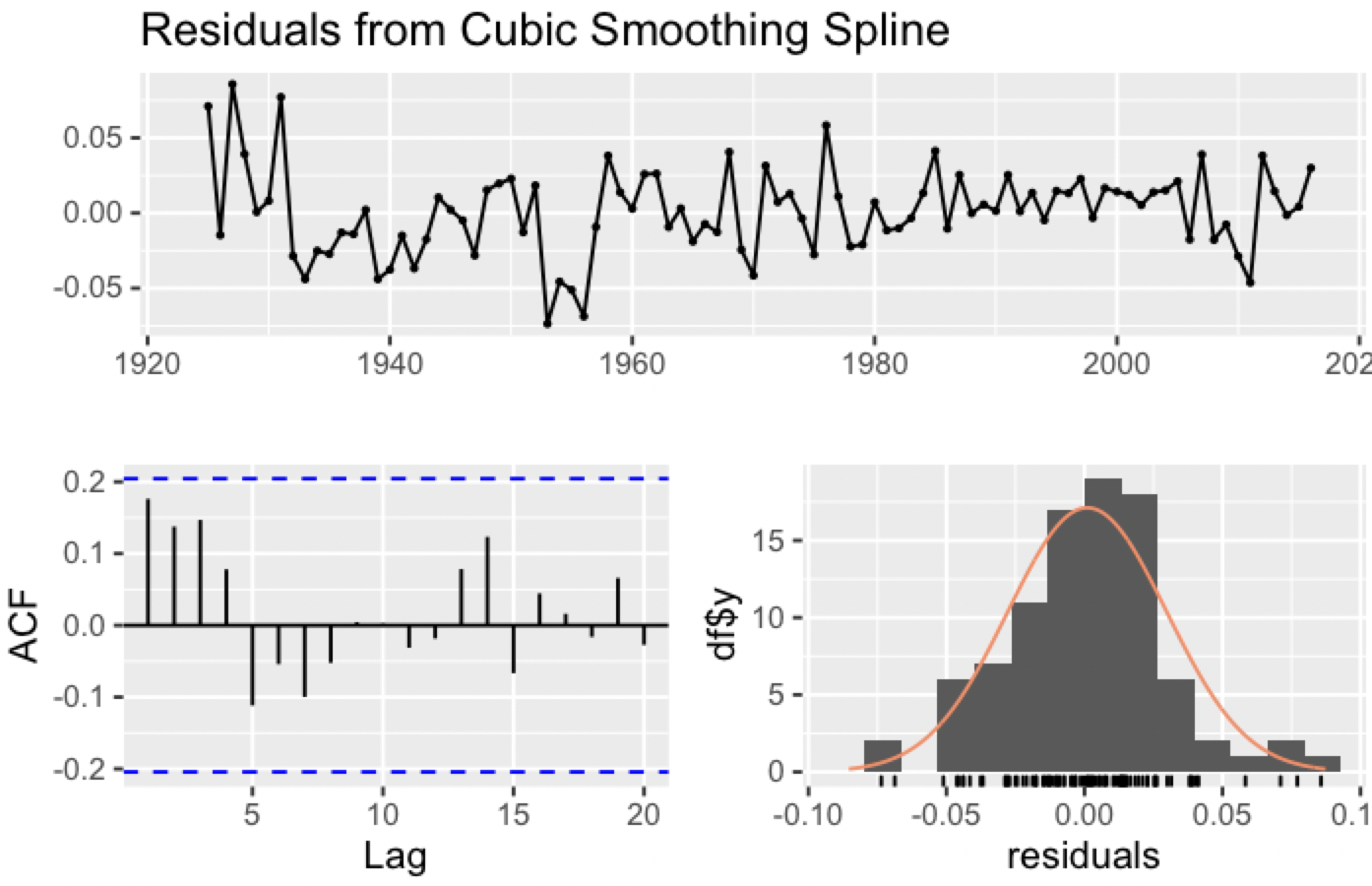
boston_men %>%
splinef(lambda=0) %>% ##램다=0으로 잔차를 변환함
checkresiduals()'Math & Statistics > Forecasting: Principles and Practice' 카테고리의 다른 글
| 챕터5 - 연습문제 (0) | 2022.03.05 |
|---|---|
| 챕터 5 - 상관관계, 인과관계, 예측 (0) | 2022.03.05 |
| 챕터 5. 예측변수 선택 (0) | 2022.02.26 |
| 챕터 5. 회귀모델평가, 예측변수 (0) | 2022.02.26 |
| 챕터 5. 회귀분석모델 - (0) | 2022.02.26 |