Forecasting: Principles and Practice 2nd Edition을 공부한 내용을 기록, 정리하고 있습니다.
5.3 회귀모델평가
관측된 y값과 예측한 y^hat 값의 차이를 잔차(residual)로 정의한다. 이 잔차는 관측값에서 모델이 예측할수 없는 부분이며, 아래의 성질을 가진다.

회귀모델을 만든 뒤에, 모델의 가정이 만족되는지 확인하기 위해 잔차를 그려보는 것이 필요하다.
잔차의 ACF 그래프
보통 현재 시점에 관측한 변수의 값은 이전 기간의 값과 비슷하거나, 그보다 이전 기간의 값과 비슷할 수 있다. 이를 보기 위해 잔차의 자기상관(autocorrelation)을 확인한다. 만약 자기상관관계가 있다고 나오면, 아직 모델이 다 잡지 못한 정보가 더 있다는 것을 의미.
잔차의 히스토그램
잔차가 정규분포를 따르는지 확인하는 좋은 방식이 히스토그램이다. 이를 통해 예측구간(prediction interval)을 쉽게 계산할 수 있다.

예측변수에 대한 잔차 그래프
예측변수(predictor variable)에 대한 잔차의 산점도(scatterplot)을 확인하여, 패턴이 없이 랜덤한지 확인한다. 만약 패턴이 보인다면, 관계가 비선형적일 수 있어 모델의 수정이 필요하다.

적합값에 대한 잔차 그래프
위에서는 예측 변수에 대한 잔차 그래프를 살펴 보았고, 이제 예측변수를 이용해서 예측한 적합값(fitted values)에 대한 잔차도 보아야 한다. 이 잔차 역시 어떤 패턴도 가지고 있으면 안되며, 만약 패턴이 나올경우 오차에 이분산성(heteroscedasticity)이 있어 잔차의 분산이 일정하지 않다는 의미이다.
cbind(Fitted = fitted(fit.consMR),
Residuals = residuals(fit.consMR)) %>%
as.data.frame() %>%
ggplot(aes(x=Fitted, y=Residuals)) + geom_point() +
xlab("적합값") + ylab("잔차")
허위회귀 (Spurious Regression)
대부분의 시계열 데이터에는 정상성(stationarity)가 나타나지 않는다. 즉 시계열의 값이 일정한 평균이나 분산으로 변하지 않는다. 정상성을 가지지 않은 시계열을 회귀분석 해버리면 허위회귀로 이어질 수 있다.
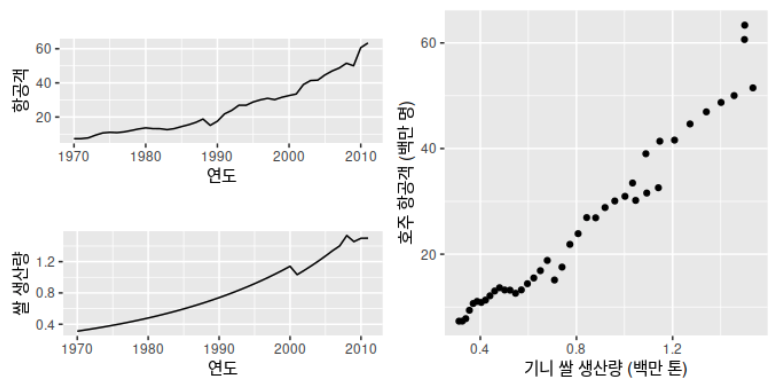
아래는 허위회귀의 예시이다. 기니의 쌀 생산량과 호주의 항공객 둘다 상승 트렌드를 가지고 있어, 관계가 있는 것처럼 보이지만, 기니의 쌀 생산량과 호주의 항공객 수는 관련이 없는 데이터이다.
5.4 예측변수들
다음은 시계열 회귀분석에 유용한 몇가지 예측변수이다.
추세 (trend)
시계열 데이터의 수체를 예측 변수로 사용해서 모델링 가능하다. tslm() 함수에서 trend 를 사용해서 추세 변수를 정할 수 있다.
가변수 (dummy variable)
원래 예측 변수는 숫자 값들을 사용하지만, 범주형(categorial) 이거나 두가지 값만 갖는 binary일수도 있다. 이런 경우 예=1, 아니오=0 이런 식으로 가변수를 만들어 사용할 수 있다.
분포된 시차값
광고 지출과 같은 값을 예측변수로 넣는 것은 유용하지만, 1회성 광고의 효과는 실제 캠페인 기간보다 오래 갈 수 있기 때문에, 광고 지출의 시차값(lagged value)를 넣는다. 시차가 증가함에 따라 계수가 감소하게 만든다.
푸리에 급수 (Fourier Series)
계절성 가변수(seasonal dummy variable)대신에 긴 계절성 주기를 가진 데이터에 사용한다. 사인과 코사인 항의 급수로, 임의의 주기의 근사치를 낸다. 푸리에 항을 쓰면 가변수가 있을 때 필요한 예측변수보다 더 적은 예측 변수를 사용하게 된다. 주로 1년 이상의 긴 주기에 대한 데이터에 유용하며, 분기별 데이터와 같은 짧은 계절성 데이터에는 계절성 가변수가 더 나은 서낵지가 될 수 있다. R에서는 fourer()함수로 구현한다.
fourier.beer <- tslm(beer2 ~ trend + fourier(beer2, K=2))
summary(fourier.beer)
#>
#> Call:
#> tslm(formula = beer2 ~ trend + fourier(beer2, K = 2))
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -42.90 -7.60 -0.46 7.99 21.79
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 446.8792 2.8732 155.53
#> trend -0.3403 0.0666 -5.11
#> fourier(beer2, K = 2)S1-4 8.9108 2.0112 4.43
#> fourier(beer2, K = 2)C1-4 53.7281 2.0112 26.71
#> fourier(beer2, K = 2)C2-4 13.9896 1.4226 9.83
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> trend 2.7e-06 ***
#> fourier(beer2, K = 2)S1-4 3.4e-05 ***
#> fourier(beer2, K = 2)C1-4 < 2e-16 ***
#> fourier(beer2, K = 2)C2-4 9.3e-15 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12.2 on 69 degrees of freedom
#> Multiple R-squared: 0.924, Adjusted R-squared: 0.92
#> F-statistic: 211 on 4 and 69 DF, p-value: <2e-16
'Math & Statistics > Forecasting: Principles and Practice' 카테고리의 다른 글
| 챕터 5 - 회귀분석, 비선형 회귀 (0) | 2022.03.05 |
|---|---|
| 챕터 5. 예측변수 선택 (0) | 2022.02.26 |
| 챕터 5. 회귀분석모델 - (0) | 2022.02.26 |
| 챕터 4. 판단 예측 (0) | 2022.02.19 |
| 챕터 3 연습문제 (0) | 2022.02.12 |