Forecasting: Principles and Practice 2nd Edition을 공부한 내용을 기록, 정리하고 있습니다.
앞에서 추세, 계절성, 주기 등의 시계열 패턴의 정의를 파악했다. 종종 추세(trend)와 주기(cycle)를 결합해서 하나의 추세-주기 성분으로 다룬다. 따라서 시계열 데이터의 성분을 나눠서 볼때, 다음의 세 가지로 나눈다. 추세(trend)-주기(cycle), 계절성(seasonality), 그리고 나머지 성분(remainder).
이제 시계열 데이터에서 시계열 성분을 추출하는 방법을 알아보자.
6.1 시계열 성분
위에서 살펴본대로, 시계열 데이터를 세 가지로 나눠서 보는 걸 덧셈 방식으로 표현하면(덧셈분해) 아래처럼 나온다. 아래 공식에서 계절성S(t), 추세 T(t), 나머지 R(t) 의 세 가지 요소를 더한 것이 시계열 데이터라고 보는 것이다.

만약 시계열 데이터를 곱셈 방식으로 표현하면(곱셈분해) 아래처럼 나타낼수도 있다. 계절성, 추세, 나머지의 곱이 시계열 데이터라고 보는 것이다.

계절성의 크기나 추세-주기 단위의 변동이 크지 않으면 덧셈분해가 유용하다. 만약 계절성 패턴의 크기나 추세-주기의 변동이 시간에 따라 변하는 것으로 보이면 곱셈분해가 더 적절할 수 있다. (예: 경제 분야 시계열)
곱셈분해가 필요할때, 곱셈분해를 사용하는 대신에 시계열 데이터를 변환해서 덧셈분해 방식으로 표현 할 수 있다. 아래는 곱셈분해를 적용하는 시계열 데이터에 로그를 씌워 덧셈분해로 바꾼 모습이다.

분해 예제: 전자장비 제조 데이터
아래 예제는 전자장비 제조 주문의 시계열 데이터이다. 빨간 선으로 표시된 것이 추세-주기를 나타낸다. 회색으로 표시된 원 데이터는 앞선 공식에서 살펴봤던 y(t)이다.

위 시계열 데이터를 분해해보면 아래 그림이 나온다. 가장 위의 그래프는 원 시계열 데이터이며, 두번째는 그 시계열 데이터의 추세, 세번째는 계절성이다. 마지막으로 나머지가 잔차로 표시된다. 각 그래프의 오른쪽에 있는 회색 막대는 각 차트별 데이터의 단위를 그린다.

위 차트에서 시계열 데이터를 세가지 파트로 발라보았고, 이제 원 데이터에서 각 파트를 하나씩 발라내면 어떤 일이 벌어지는지 확인해보자. 가장 먼저, 계절성을 제거해보자. 아래 그림을 보면 아래위로 오가는 계절성 진폭이 줄어든 모습을 파란 선으로 확인할 수 있다. 만약 추세-주기를 확인하고 싶으나 계절성으로 인한 변동을 고려하고 싶지 않다면, 이런 계절성 조정 데이터(seasonality adjusted data)가 쓰기 편하다. 아래 그래프에서 계절성은 제거되었지만, 아직 추세-주기와 나머지 성분이 있다.

6.2 이동평균(Moving Average)
고전적인 시계열 분해 방법의 하나로, 추세-주기를 측정하는데 많이 사용되는 것이 이동평균이다.
이동평균 평활(Moving Average Smoothing)
m차수 데이터의 이동평균은 아래처럼 쓴다. k기간 동안의 시계열 값을 평균내어 추세-주기를 결정한다. 이런 방식의 이동평균을 차수 m의 이동평균이라는 뜻으로 m-MA라고 부르기도 한다. m값은 2k+1로, 특정 날짜나 시간의 앞뒤로 k만큼 데이터를 잘라서 평균내어 가져오는 방식이다.

아래는 5년 m-MA의 예시이다. 처음 2년과 마지막 2년은 데이터가 비게 된다. 1991년의 5-MA는 1989~1993년의 5개년의 데이터를 평균낸 값이다. 이동평균선은 원 데이터보다 비교적 매끄러운 모습을 가졌다.

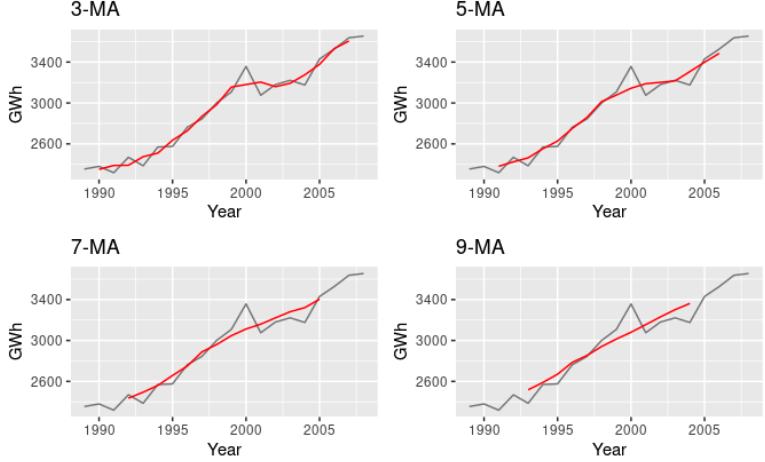
m-MA에서 m의 개수가 커질 수록 양 끝에 비는 값이 늘어나고, 이동평균선이 더 납작해진다. 아래 그림은 k값을 3, 5, 7, 9 로 각각 잡고 같은 데이터에 대한 이동평균선을 구해본 그림이다. m값이 홀수라면 이렇게 쉽게 구할 수 있지만, m값이 짝수라면 더이상 대칭이 되지 않기 때문에 문제가 생긴다.
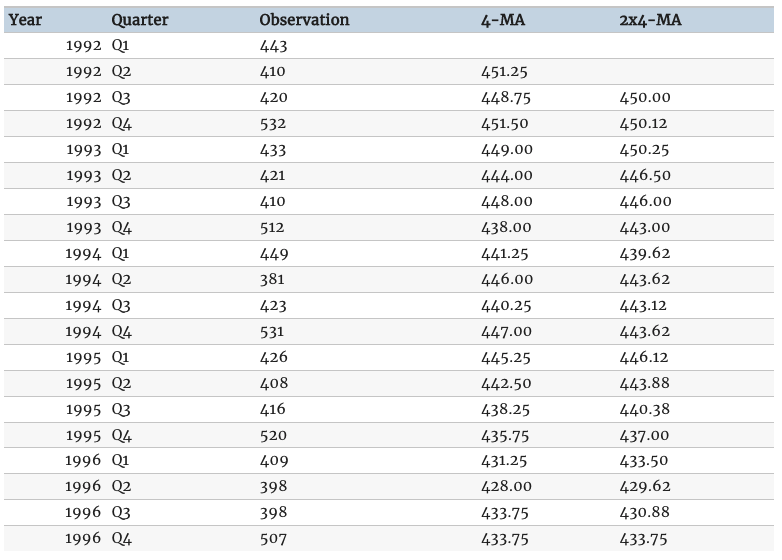
그러면 m값이 짝수이면 어떻게 하나..? 이동평균에 또 이동평균을 사용할 수 있다. 예를 들어, m값을 4로 잡아 MA를 계산해보자. 그리고 나온 값을 가지고 m값을 2로 잡아서 MA를 또 계산해보자. 그러면 대강 아래 테이블처럼 나온다. 2*4 - MA이며, m이 홀수일때처럼 대칭적인 모양으로 만들어진다.
이 원리를 수식으로 풀이해보면 아래처럼 된다. 괄호 안에 있는 4-MA 값 두개의 평균이 2-MA와 동일하다. 수식으로 풀어내면 y(t-2), y(t-1), y(t), y(t+1), y(t+2)의 5가지 항으로 변하며 대칭적인 모습으로 변하는 것을 확인할 수 있다. 이를 중심화된 이동평균(centered MA)라고 부르며, 각 관측값들에는 1/8, 1/4의 가중치가 매겨져 있는 가중평균이라고도 볼 수 있다. 짝수 m-MA를 대칭으로 만들기 위해서는 짝수 m-MA를 중복 사용해야 하며, 같은 이유로 홀수 m-MA에 m-MA를 또 중복 사용하고자 한다면 두번째 사용하는 m값도 홀수여야 한다.

가중 이동평균 (weighted MA)
계절성 데이터에서 추세-주기를 측정하기
중심화된 이동평균 (centered MA)의 주요 용도는 계절성이 있는 데이터에서 추세-주기를 확인하는 데 있다. 방금 위에서 찾아본 2*4-MA의 공식을 살펴보자. 아래 공식을 분기별 데이터처럼 4개로 나눠지는 계절성 데이터에 적용하면, y(t-2), y(t+2)의 두 항은 앞뒤연도의 영향을 받게 된다. 예를 들어, y(t) = 3분기라면, y(t-2) = 1분기 (올해)가 되고, y(t+2)는 내년의 1분기가 된다. 올해와 내년의 1분기를 같은 가중치를 줌으로써 계절성의 변동치를 없앨수 있다. 이와 같은 방식을 m+1차수의 가중 이동평균이라고 한다. m+1차수의 가중이동평균 2*m-MA를 구할 때는 첫번째와 마지막값은 1/(2m), 나머지는 1/m의 가중치를 주게 된다. 계절성 주기가 짝수이면 2*m-MA, 홀수이면 m-MA를 사용한다.
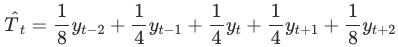
이처럼 이동평균의 조합은 가중이동평균이 된다. 가중치를 모두 더하면 1이 되며, 가중치들은 대칭적이다. 가중평균의 장점은 매끄러운 추세-주기(trend-cycle) 값을 얻을 수 있다는 것이다.
6.3 고전적인 분해법
고전적인 분해법은 단순하고, 위에서 소개한 대로 덧셈과 곱셈 분해가 있다. 고전적인 분해는 계절적인 성분이 매년 일정하다고 가정한다. 따라서 분기별 데이터에서는 m=4, 월별 데이터에서는 m=12, 주별 패턴이 있는 일별 데이터에서는 m=7로 잡는다.
덧셈분해
- 추세-주기 성분 T(t) 계산하기: m이 짝수이면 2*m-MA 사용, 홀수이면 m-MA 사용
- 데이터에서 방금 구한 추세-주기 성분을 빼준다. y(t) - T(t) = S(t) + R(t)
- y(t) - T(t)의 평균을 구해 계절성분 S(t) 를 구한다.
- S(t)도 발라내고 남은 값이 나머지 성분이 된다. y(t) - T(t) - S(t) = R(t)
계절성분 구하는 예시: 월별 데이터를 구할때, 월별 계절성분은 데이터에서 추세를 제거한 모든 월별 평균이 된다.
곱셈분해
- 덧셈분해 법과 비슷하게 구한다. 대신 뺄셈 대신 나눗셈을 사용한다는 차이가 있다.
- 추세-주기 성분 T(t) 계산하기: 위와 동일하게 m이 짝수이면 2*m-MA 사용, 홀수이면 m-MA 사용
- y(t)에서 추세를 발라낼때, 뺄셈 대신 나눗셈 y(t)/T(t) 를 사용한다.
- 이제 계절성분을 측정하기 위해, y(t)/T(t)의 평균을 구한다. 계절성분의 값이 m에 가까워지게 조정.
- 마지막으로 계절성분도 나눠주어 나머지 성분을 계산한다. R(t) = y(t)/[T(t)S(t)]
고전적인 분해의 단점
- 첫 관측값과 마지막 값에 대해 추세 추정값을 구할수 없다. 예를 들면, m=12일때 추세를 추정하기 위해 데이터가 앞뒤로 12씩 필요하므로 1~6, (n-6)~n의 추세 추정값은 구할 수 없다.
- 추세-주기 측정을 할때 데이터에 나타나는 급격한 증가나 감소를 제대로 반영하지 못한다. 따라서 과도하게 데이터가 매끄러워진다.
- 계절성분이 매년 나타난다는 가정하에 적용하기 때문에, 1년보다 더 긴 시계열에서는 잘 맞지 않기도 한다. 시간이 오래 지남에 따라 변화하는 데이터를 잘 반영하지 못한다.
- 짧은 기간동안 예외적인 사건(outlier 비슷한)이 일어나면 잘 반영하지 못한다.
6.4 X11 분해
X11 기법은 미국 인구 조사국과 캐나다 통계청에서 고안한 방법으로, 분기별 데이터와 월별 데이터를 분해할 때 쓰인다. 고전적인 분해의 단점을 조금 보완한 방식이다. 고전적인 분해와 X11분해의 비교를 해보자.
먼저, 아래 코드를 돌리면 고전적인 분해를 해 준다. remainder가 1에 가까울수록 잘 분해된 것인데, 고전적인 분해의 경우 2009년 쯤에 갑자기 나머지가 커진다. 추세가 급격하게 감소하는 지점인데, data와 trend 그래프를 비교하면 해당 시점에 원 데이터에 비해 추세가 더 빠르게 감소하고 있다.
elecequip %>% decompose(type="multiplicative") %>%
autoplot() + xlab("Year") +
ggtitle("Classical multiplicative decomposition
of electrical equipment index")
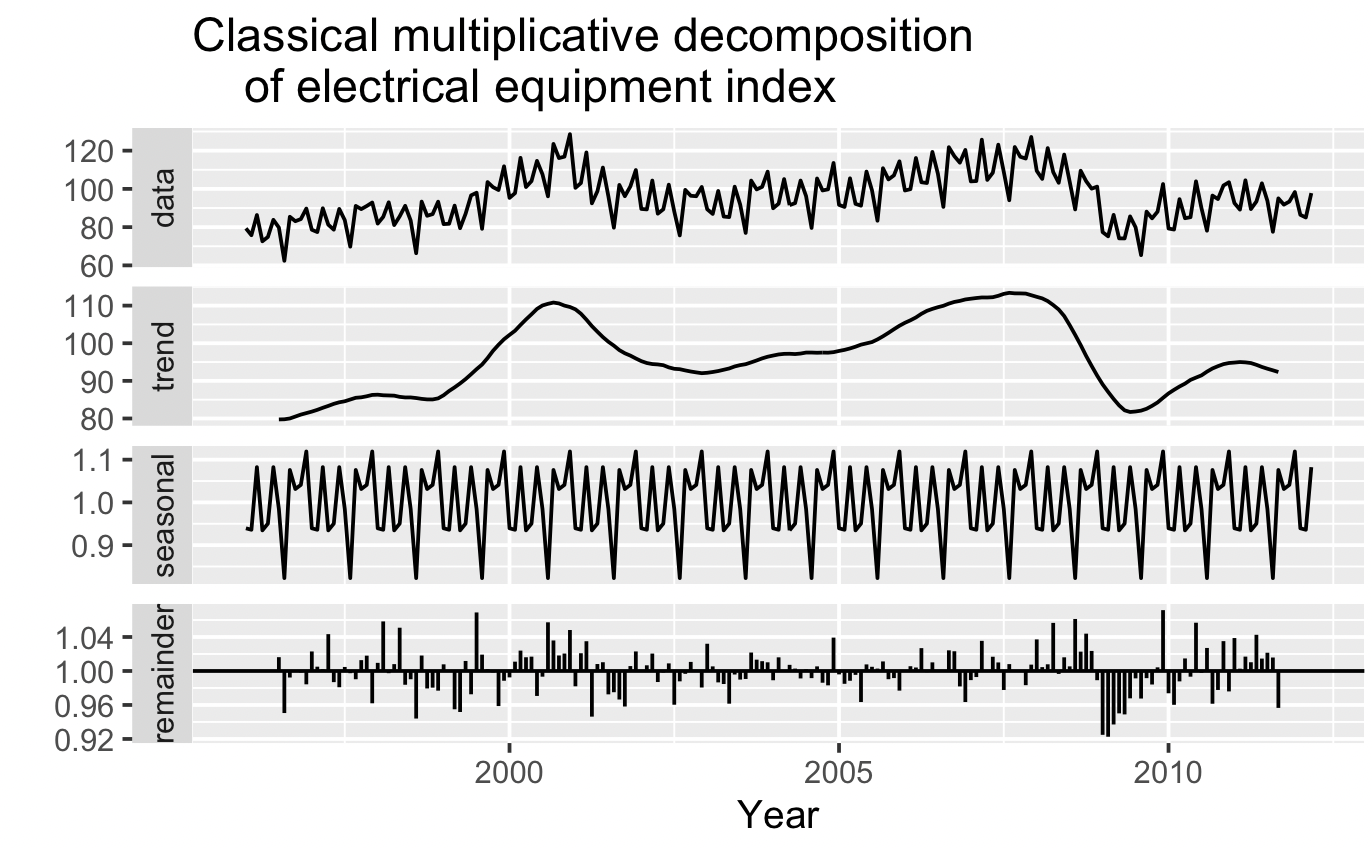
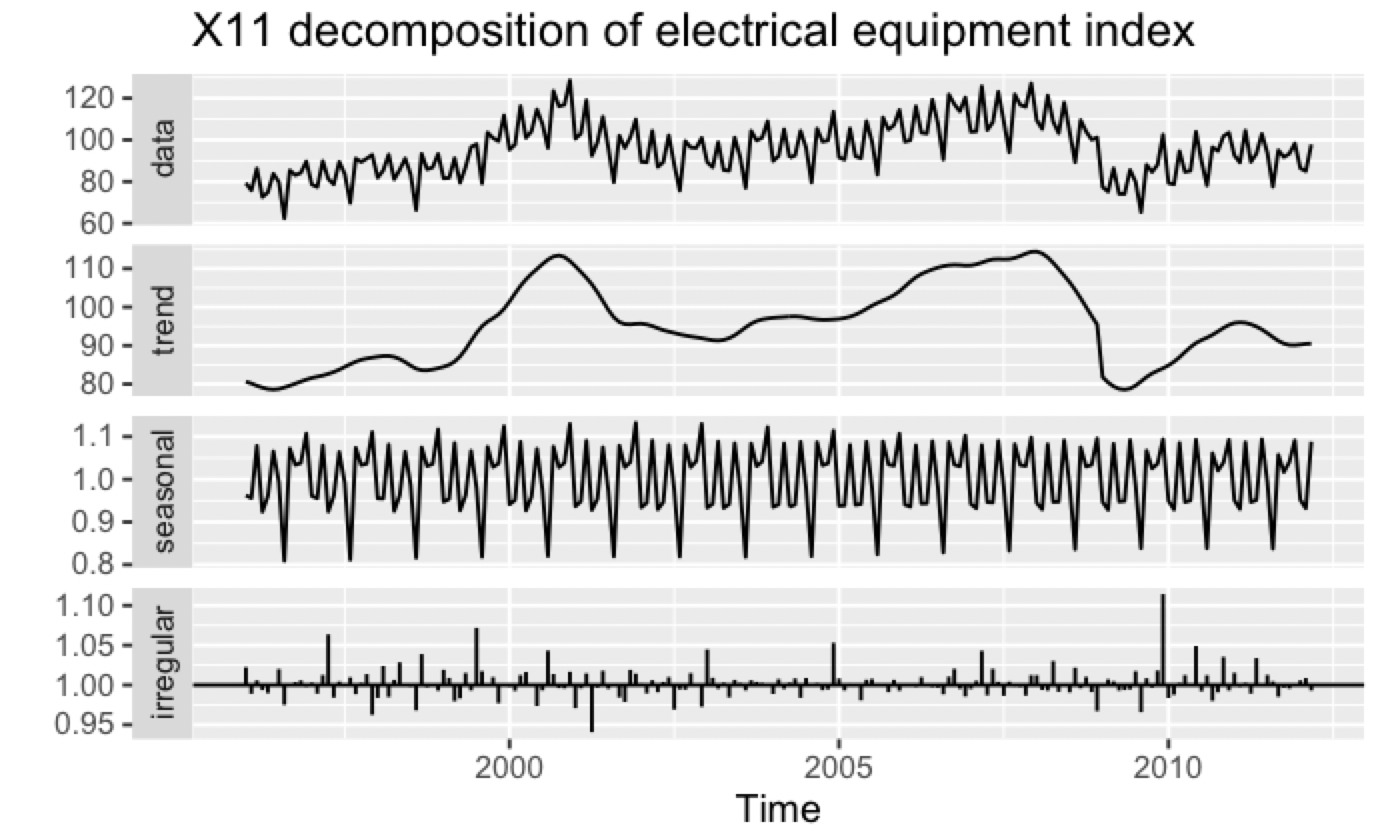
아래는 X11 분해를 사용한 예시이다. 위에서 2009년쯤 크게 발생한 remainder가 많이 줄어든 것을 볼 수 있다.
## seasonal, x13binary 패키지들을 설치해야 한다
library(seasonal)
elecequip %>% seas(x11="") -> fit
autoplot(fit) +
ggtitle("X11 decomposition of electrical equipment index")
6.5 SEATS 분해
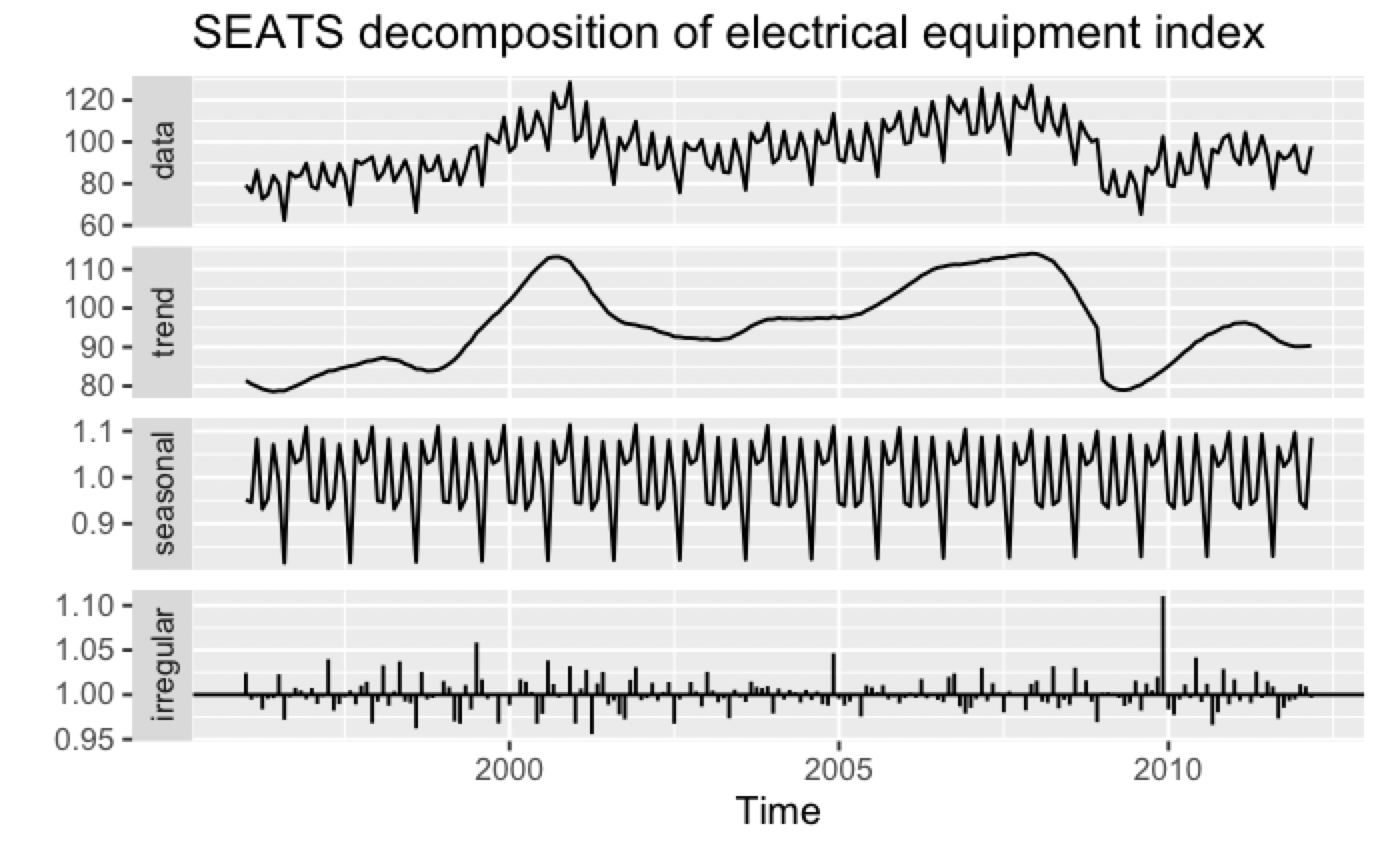
Seasonal Extraction in ARIMA Time Series (ARIMA 시계열에서 계절성 추출)의 줄임말이다. 분기별 데이터와 월별 데이터에서만 작동하며, 일별, 시간별 등 다른 종류의 계절성은 다른 접근방식으로 다루어야 한다. 좀전에 살펴본 X11과 비슷한 방식이다. 이 책에서는 다루지 않으며, R 예시만 주어져 있다.
library(seasonal)
elecequip %>% seas() %>%
autoplot() +
ggtitle("SEATS decomposition of electrical equipment index")
'Math & Statistics > Forecasting: Principles and Practice' 카테고리의 다른 글
| 7. 지수 평활 - part 1 (0) | 2022.07.09 |
|---|---|
| 챕터 6 시계열 분해 - 파트 2 (0) | 2022.03.19 |
| 챕터5 - 연습문제 (0) | 2022.03.05 |
| 챕터 5 - 상관관계, 인과관계, 예측 (0) | 2022.03.05 |
| 챕터 5 - 회귀분석, 비선형 회귀 (0) | 2022.03.05 |